- Published on
In-depth Analysis of C++ STL Source Code: Doubly Linked Circular List (list)
- Authors

- Name
- light-city
In-depth Analysis of C++ STL Source Code: Doubly Linked Circular List (list)
Table of Contents
0. Introduction
The corresponding version of the source code is gcc-4.9.1.
1. list
A list is a doubly linked circular list with the following structure:
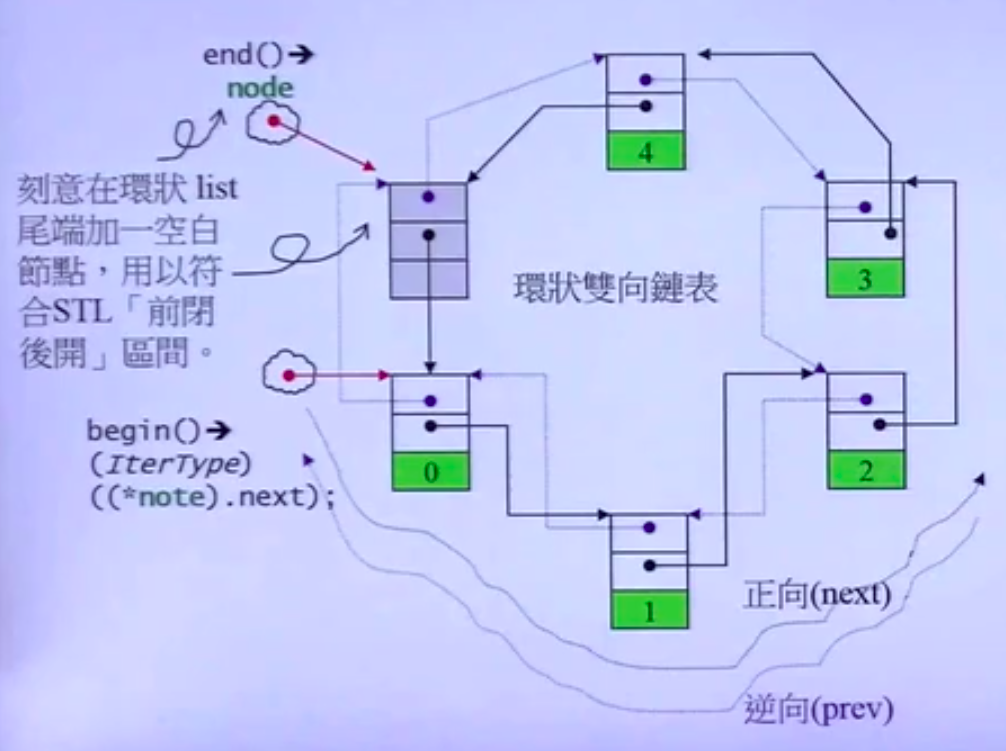
The self-drawn diagram is as follows:
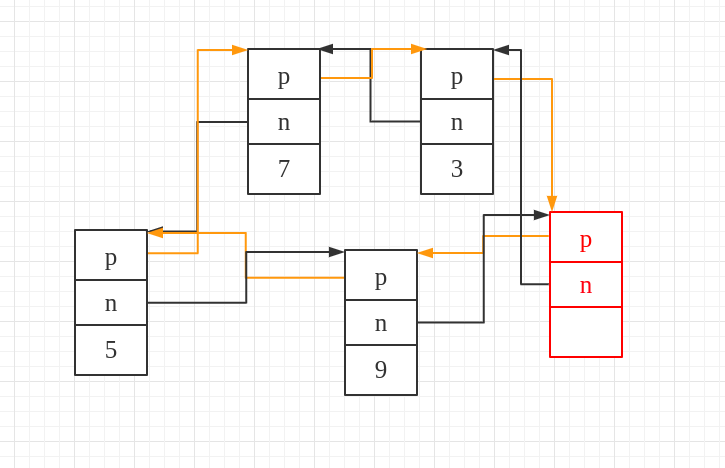
The doubly linked circular list starts inserting from the node with the value 3, and the red box represents the last node (the node pointed to by end()). The yellow lines represent pointers to the predecessor nodes, and the black lines represent pointers to the successor nodes.
1.1 List Source Code
1.1.1 Class Structure
template<typename _Tp, typename _Alloc = std::allocator<_Tp> >
class list : protected _List_base<_Tp, _Alloc>
{
}
The list class inherits from _List_base.
1.1.2 Implementation of Doubly Linked Circular List
【Constructor】
(1) List without any elements
explicit
list(const allocator_type &__a) _GLIBCXX_NOEXCEPT: _Base(_Node_alloc_type(__a)) {}
(2) List with n elements and initial values
explicit list(size_type __n, const value_type &__value = value_type(),const allocator_type &__a = allocator_type()) : _Base(_Node_alloc_type(__a))
{ _M_fill_initialize(__n, __value); }
(3) Initialize list from a range
template<typename _InputIterator>
list(_InputIterator __first, _InputIterator __last,
const allocator_type &__a = allocator_type())
: _Base(_Node_alloc_type(__a)) {
// Check whether it's an integral type. If so, it's not an iterator.
typedef typename std::__is_integer<_InputIterator>::__type _Integral;
_M_initialize_dispatch(__first, __last, _Integral());
}
【Creating Nodes】
Tasks: Create a new node and dynamically allocate memory, then return the node.
_Node *_M_create_node(const value_type &__x) {
_Node *__p = this->_M_get_node();
__try
{
_M_get_Tp_allocator().construct
(std::__addressof(__p->_M_data), __x);
}
__catch(...)
{
_M_put_node(__p);
__throw_exception_again;
}
return __p;
}
It's important to note that there are two crucial functions inside: _M_get_node and _M_put_node. Upon further examination, it's found that these methods come from the base class. The source code is as follows:
_List_node<_Tp> * _M_get_node() { return _M_impl._Node_alloc_type::allocate(1); }
void _M_put_node(_List_node<_Tp> *__p) _GLIBCXX_NOEXCEPT
{ _M_impl._Node_alloc_type::deallocate(__p, 1); }
These functions are responsible for dynamically allocating memory to create a node. If an exception is thrown during the creation process, the memory is deallocated.
【Inserting Nodes】
Inserting nodes includes:
- Inserting n nodes with specified values at the end, corresponding to the function
_M_fill_initialize, which is used in the list's constructor:
explicit list(size_type __n, const value_type &__value = value_type(),const allocator_type &__a = allocator_type()) : _Base(_Node_alloc_type(__a))
{ _M_fill_initialize(__n, __value); }
- Inserting a node with a specified value at a specific position, corresponding to the function
_M_insert. The commonly usedpush_backandpush_frontfunctions actually call the_M_insertfunction underneath.
The difference between the two functions is:
this->_M_insert(end(), __x); // push_back insert at the end
this->_M_insert(begin(), __x); // push_front insert at the beginning
- Most important: Doubly Linked Circular List Insertion Function
_M_hook
As mentioned earlier, push_back, push_front, _M_insert, and insert are all implemented using the most fundamental doubly linked list insertion function, _M_hook.
Let's delve deeper into this:
The _M_fill_initialize source code is as follows:
void _M_fill_initialize(size_type __n, const value_type &__x) {
for (; __n; --__n)
push_back(__x);
}
The push_back source code is as follows:
void push_back(const value_type &__x) { this->_M_insert(end(), __x); }
The _M_insert function inserts a node with the initial value of x at the specified position.
void _M_insert(iterator __position, const value_type &__x) {
_Node *__tmp = _M_create_node(__x);
__tmp->_M_hook(__position._M_node);
}
The _M_hook implementation is found in gcc-4.9.1/libstdc++-v3/src/c++98/list.cc. Of course, other functions of _List_node_base, such as _M_unhook, are also found in this file.
// Insert this node before the specified position
void _List_node_base::_M_hook(_List_node_base* const __position) _GLIBCXX_USE_NOEXCEPT
{
this->_M_next = __position;
this->_M_prev = __position->_M_prev;
__position->_M_prev->_M_next = this;
__position->_M_prev = this;
}
From the above code, we can see that the function _M_hook is used to insert a node before the specified position. For example, inserting a node with the value 9 before the node with position 7. The specific steps of insertion are illustrated in the diagram below.
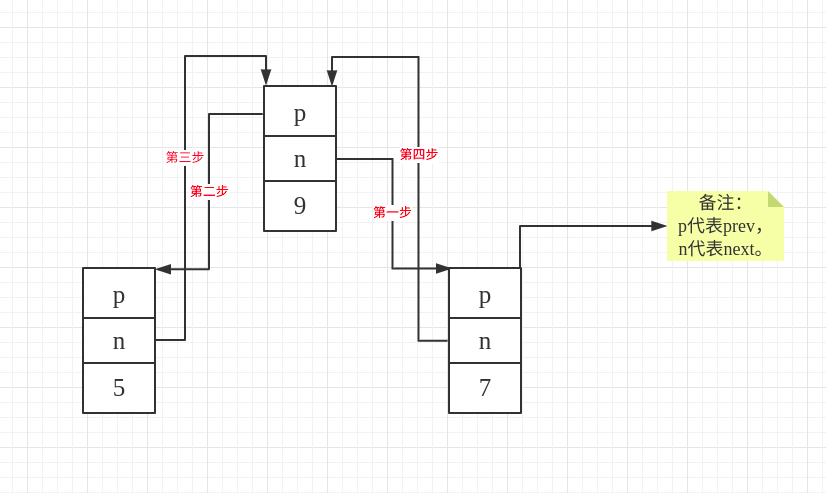
When analyzing the above code, we know that splice is to insert the entire list represented by the above diagram in front of the specified iterator. For example, if we want to insert before the following two nodes, the specific graphical steps are as follows:
this represents the node with the value 8, and the diagram below illustrates inserting the entire list between nodes 10 and 8.
__last represents the node in the red box, which is the node pointed to by end(). We don't need this node, so it will be removed from the entire list during the subsequent processing.
Step 1: First, set the next pointer of the previous valid node, which is the node in the red box, to point to the specified node 8.
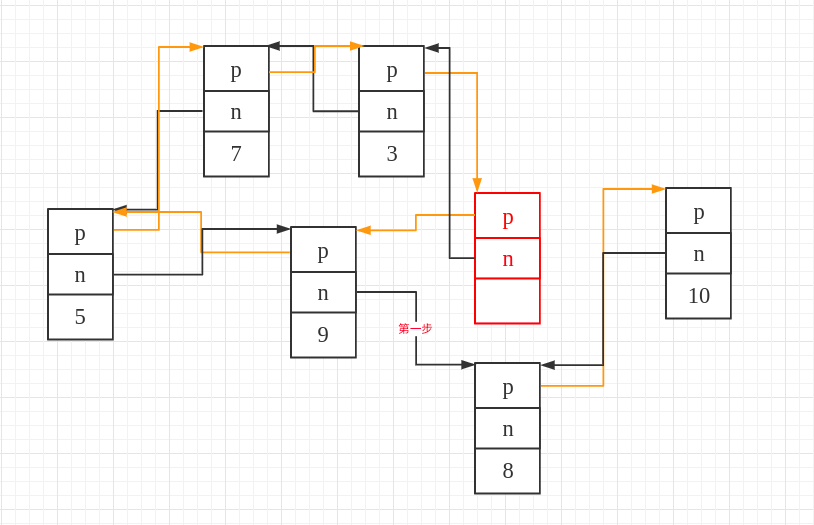
The corresponding code is:
__last->_M_prev->_M_next = this;
Step Two: The next pointer of _last points to itself.

The corresponding code is:
__first->_M_prev->_M_next = __last;
Step Three: Make the next pointer of the node before the specified iterator point to the original first node (__first) of the list.
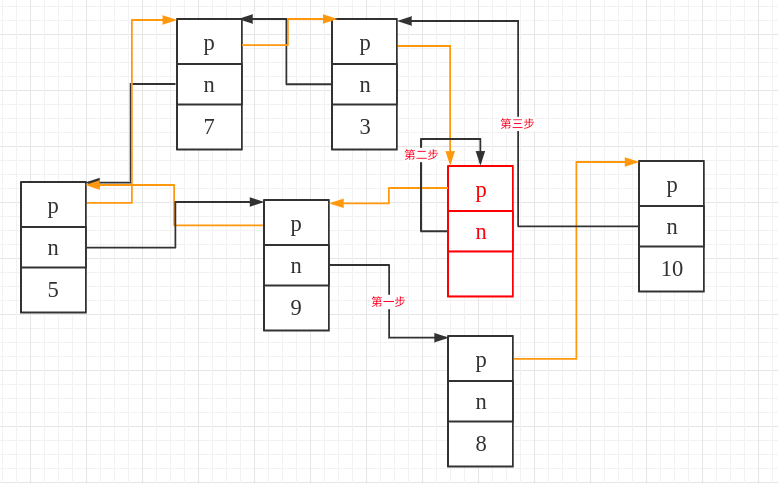
The corresponding code is:
this->_M_prev->_M_next = __first;
Step Four: Save the predecessor node of the specified iterator (corresponding to the node with a value of 10 in the diagram).
_List_node_base* const __tmp = this->_M_prev;
Step Five: Make the predecessor node of the specified iterator point to the actual last node of the original list (the node before end()).
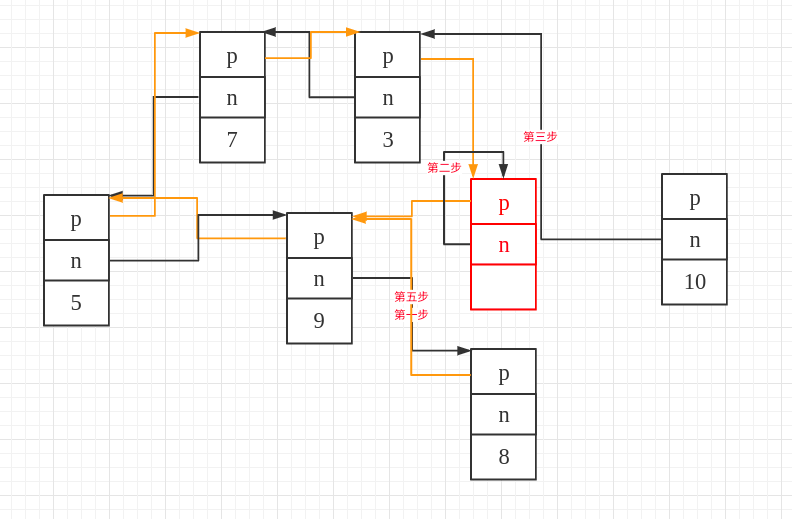
The corresponding code is:
this->_M_prev = __last->_M_prev;
Step Six: Make the prev pointer of the last node of the original list (pointed by end()) point to itself.

The corresponding code is:
__last->_M_prev = __first->_M_prev;
Step Seven: Make the prev pointer of the first node of the original list point to the node saved in step four.
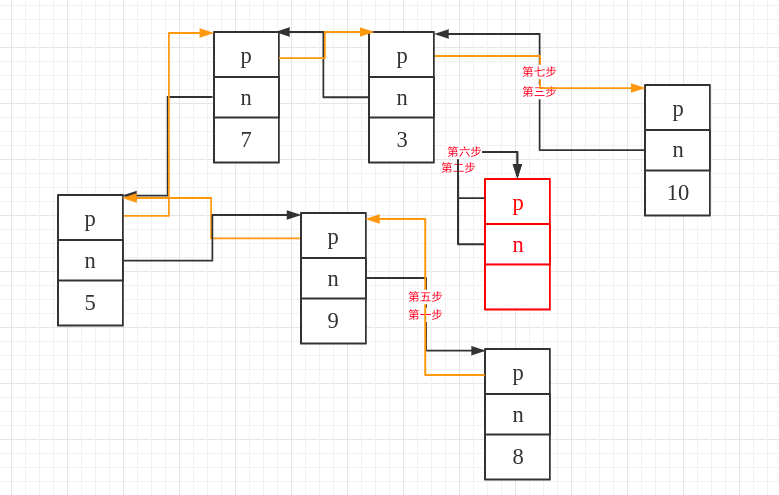
The corresponding code is:
__first->_M_prev = __tmp;
By performing the above seven steps, inserting a list between node 8 and node 10 is completed.
- Step Three: Insert data from a list range before the specified iterator.
template<typename _InputIterator>
void
insert(iterator __position, _InputIterator __first,
_InputIterator __last) {
list __tmp(__first, __last, get_allocator());
splice(__position, __tmp);
}
The principle is the same as above, except that this __tmp calls another constructor.
Deleting Nodes
- Deleting a specified node
Deleting a specified node is divided into two methods: deleting by iterator and deleting by element value.
(1) Deleting by iterator, corresponding function is erase
Where pop_front and pop_back, erase, remove are implemented based on the _M_erase function.
this->_M_erase(begin()); // Continuously delete elements at the beginning with pop_front
this->_M_erase(iterator(this->_M_impl._M_node._M_prev)); // Remove the last element with pop_back
In libstdc++-v3/include/bits/list.tcc:
erase(iterator __position)
#endif
{
iterator __ret = iterator(__position._M_node->_M_next);
_M_erase(__position._M_const_cast());
return __ret;
}
(2) Deleting by element value, corresponding function is remove
Special case handling: when the address of the deleted element is the same as the iterator's address, save it first, and finally check if the saved iterator is not end(), if not, delete it. The underlying operation is still through _M_erase.
template<typename _Tp, typename _Alloc>
void list<_Tp, _Alloc>::remove(const value_type& __value)
{
iterator __first = begin();
iterator __last = end();
iterator __extra = __last;
while (__first != __last)
{
iterator __next = __first;
++__next;
if (*__first == __value)
{
if (std::__addressof(*__first) != std::__addressof(__value))
_M_erase(__first);
else
__extra = __first;
}
__first = __next;
}
if (__extra != __last)
_M_erase(__extra);
}
In addition to this remove, there is also a remove_if, which deletes based on conditions.
template<typename _Tp, typename _Alloc>
template <typename _Predicate>
void list<_Tp, _Alloc>::
remove_if(_Predicate __pred)
{
iterator __first = begin();
iterator __last = end();
while (__first != __last)
{
iterator __next = __first;
++__next;
if (__pred(*__first))
_M_erase(__first);
__first = __next;
}
}
Simply remove the if condition in the above remove and add a judgment inside.
Usage example:
bool isone(int one) {
return one==2;
}
int main() {
list<int> t;
t={3,4,0,2,0,10,10};
t.remove_if(isone);
}
- Deleting a series of nodes
- Deleting all nodes, corresponding function is
clear
(1) Detailed analysis of deleting specified nodes
_M_erase(iterator __position)
_GLIBCXX_NOEXCEPT
{
__position._M_node->_M_unhook();
_Node *__n = static_cast<_Node *>(__position._M_node);
#if __cplusplus >= 201103L
_M_get_Node_allocator().destroy(__n);
#else
_M_get_Tp_allocator().destroy(std::__addressof(__n->_M_data));
#endif
_M_put_node(__n); // Free memory
}
Where _M_unhook is implemented in gcc-4.9.1/libstdc++-v3/src/c++98/list.cc, as follows:
void _List_node_base::_M_unhook() _GLIBCXX_USE_NOEXCEPT
{
_List_node_base* const __next_node = this->_M_next; // Step one: save the successor node
_List_node_base* const __prev_node = this->_M_prev; // Step two: save the predecessor node
__prev_node->_M_next = __next_node; // Step three: the predecessor node's next points to the successor node
__next_node->_M_prev = __prev_node; // Step four: the successor node's prev points to the predecessor node
}
For example: Deleting the node with a value of 9, diagrams for steps three and four:
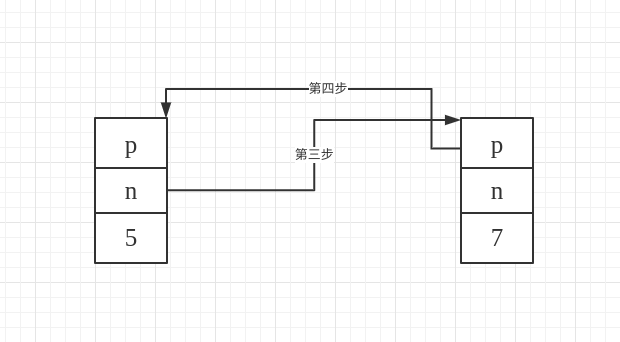
(2) Detailed analysis of deleting a series of elements
iterator
#if __cplusplus >= 201103L
erase(const_iterator __first, const_iterator __last) noexcept
#else
erase(iterator __first, iterator __last)
#endif
{
while (__first != __last)
__first = erase(__first);
return __last._M_const_cast();
}
Use erase to delete data within the given iterator range.
(3) Detailed analysis of deleting all elements
Empty the elements and initialize, returning the list to its default state.
void clear()
_GLIBCXX_NOEXCEPT
{
_Base::_M_clear();
_Base::_M_init();
}
// Translate to English
Empty the elements and initialize, returning the list to its default state.
```cpp
void clear()
_GLIBCXX_NOEXCEPT
{
_Base::_M_clear();
_Base::_M_init();
}
Where _M_clear implementation resides in: libstdc++-v3/include/bits/list.tcc:
_List_base<_Tp, _Alloc>::
_M_clear() _GLIBCXX_NOEXCEPT
{
typedef _List_node<_Tp> _Node;
_Node* __cur = static_cast<_Node*>(_M_impl._M_node._M_next);
while (__cur != &_M_impl._M_node)
{
_Node* __tmp = __cur; // Save the node
__cur = static_cast<_Node*>(__cur->_M_next); // Traverse forward
#if __cplusplus >= 201103L
_M_get_Node_allocator().destroy(__tmp);
#else
_M_get_Tp_allocator().destroy(std::__addressof(__tmp->_M_data));
#endif
_M_put_node(__tmp); // Free memory
}
}
_M_init implementation, all pointing to itself.
void _M_init()
_GLIBCXX_NOEXCEPT
{
this->_M_impl._M_node._M_next = &this->_M_impl._M_node;
this->_M_impl._M_node._M_prev = &this->_M_impl._M_node;
}
【Element Access】
Each has two versions: reference and const reference.
- front returns the first element
reference front()
_GLIBCXX_NOEXCEPT
{ return *begin(); }
const_reference
front() const
_GLIBCXX_NOEXCEPT
{ return *begin(); }
- returns the last element
reference
back()
_GLIBCXX_NOEXCEPT
{
iterator __tmp = end();
--__tmp;
return *__tmp;
}
const_reference
back() const
_GLIBCXX_NOEXCEPT
{
const_iterator __tmp = end();
--__tmp;
return *__tmp;
}
【Algorithms】
- unique
Removes all but the first element from every consecutive group of equal elements in the container.
Note that only elements that are immediately next to each other are compared, so this function is especially useful for sorted lists.
template<typename _Tp, typename _Alloc>
template <typename _BinaryPredicate>
void
list<_Tp, _Alloc>::
unique(_BinaryPredicate __binary_pred)
{
iterator __first = begin();
iterator __last = end();
if (__first == __last)
return;
iterator __next = __first;
while (++__next != __last)
{
// If condition is met, delete
if (__binary_pred(*__first, *__next))
// Delete
_M_erase(__next);
else
__first = __next;
__next = __first;
}
}
Example usage:
// list::unique
#include <iostream>
#include <cmath>
#include <list>
// a binary predicate implemented as a function:
bool same_integral_part (double first, double second)
{ return ( int(first)==int(second) ); }
// a binary predicate implemented as a class:
struct is_near {
bool operator() (double first, double second)
{ return (fabs(first-second)<5.0); }
};
int main ()
{
double mydoubles[]={ 12.15, 2.72, 73.0, 12.77, 3.14,
12.77, 73.35, 72.25, 15.3, 72.25 };
std::list<double> mylist (mydoubles,mydoubles+10);
mylist.sort(); // 2.72, 3.14, 12.15, 12.77, 12.77,
// 15.3, 72.25, 72.25, 73.0, 73.35
mylist.unique(); // 2.72, 3.14, 12.15, 12.77
// 15.3, 72.25, 73.0, 73.35
mylist.unique (same_integral_part); // 2.72, 3.14, 12.15
// 15.3, 72.25, 73.0
mylist.unique (is_near()); // 2.72, 12.15, 72.25
std::cout << "mylist contains:";
for (std::list<double>::iterator it=mylist.begin(); it!=mylist.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
return 0;
}
The above will remove all duplicate elements after sorting, leaving only one, whereas without sorting it will only remove duplicate and consecutive elements.
- merge
The merge implementation utilizes the _M_transfer function. Assuming there are two lists, list1 and list2. Elements in list1 are compared with those in list2. If the element in list1 is smaller than that in list2, list1 iterator is incremented without any operation. If the element in list1 is greater than that in list2, the smaller element from list2 is inserted into list1 using the _M_transfer function, effectively inserting it before the iterator that was being compared in list1. This process is repeated until all elements are merged into list1.
When list1 is fully traversed while list2 is not, only one _M_transfer is executed to insert the remaining elements in list2 from the current iterator to the end into list1.
template<typename _Tp, typename _Alloc>
void
list<_Tp, _Alloc>::
#if __cplusplus >= 201103L
merge(list&& __x)
#else
merge(list& __x)
#endif
{
// _GLIBCXX_RESOLVE_LIB_DEFECTS
// 300. list::merge() specification incomplete
if (this != &__x)
{
_M_check_equal_allocators(__x);
iterator __first1 = begin();
iterator __last1 = end();
iterator __first2 = __x.begin();
iterator __last2 = __x.end();
while (__first1 != __last1 && __first2 != __last2)
if (*__first2 < *__first1)
{
iterator __next = __first2;
_M_transfer(__first1, __first2, ++__next);
__first2 = __next;
}
else
++__first1;
if (__first2 != __last2)
_M_transfer(__last1, __first2, __last2);
}
}
Usage:
int main() {
list<int> l1 = {2,3,5,7};
list<int> l2 = {1,10,9,5};
l1.sort();
l2.sort();
l1.merge(l2);
return 0;
}
- sort
Since the sort algorithm in STL accepts input iterators as random access iterators, but bidirectional list container access is via bidirectional iterators, the STL sort algorithm cannot be used directly. Instead, a custom sorting algorithm specific to bidirectional iterators must be defined. From the source code analysis, we can see that this sorting algorithm is similar to merge sort.
In sort, the splice function is called as:
void splice(const_iterator __position, list& __x, const_iterator __i) noexcept
{ splice(__position, std::move(__x), __i); }
Further analysis:
void
splice(iterator __position, list &__x, iterator __i)
{
iterator __j = __i._M_const_cast();
++__j;
if (__position == __i || __position == __j)
return;
if (this != &__x)
_M_check_equal_allocators(__x);
this->(__position._M_const_cast(),
__i._M_const_cast(), __j);
}
Finally, _M_transfer is called.
In sort, there is also a swap function to swap two lists, with the implementation in gcc-4.9.1/libstdc++-v3/src/c++98/list.cc:
void
_List_node_base::swap(_List_node_base& __x,
_List_node_base& __y) _GLIBCXX_USE_NOEXCEPT
{
if ( __x._M_next != &__x )
{
if ( __y._M_next != &__y )
{
// Both __x and __y are not empty.
std::swap(__x._M_next,__y._M_next);
std::swap(__x._M_prev,__y._M_prev);
__x._M_next->_M_prev = __x._M_prev->_M_next = &__x;
__y._M_next->_M_prev = __y._M_prev->_M_next = &__y;
}
else
{
// __x is not empty, __y is empty.
__y._M_next = __x._M_next;
__y._M_prev = __x._M_prev;
__y._M_next->_M_prev = __y._M_prev->_M_next = &__y;
__x._M_next = __x._M_prev = &__x;
}
}
else if ( __y._M_next != &__y )
{
// __x is empty, __y is not empty.
__x._M_next = __y._M_next;
__x._M_prev = __y._M_prev;
__x._M_next->_M_prev = __x._M_prev->_M_next = &__x;
__y._M_next = __y._M_prev = &__y;
}
}
The specific implementation swaps the next and prev pointers based on whether the lists are empty or not.
Now let's take a look at the powerful sort:
template<typename _Tp, typename _Alloc>
void
list<_Tp, _Alloc>::sort() {
// Do nothing if the list has length 0 or 1.
if (this->_M_impl._M_node._M_next != &this->_M_impl._M_node
&& this->_M_impl._M_node._M_next->_M_next != &this->_M_impl._M_node) {
list __carry; // Auxiliary list used to extract elements from 'this' and temporarily store the merge result of two lists
list __tmp[64]; // Stores the result of each merge level, where the i-th list stores 2^i elements or 0
list *__fill = &__tmp[0]; // Represents the current maximum merge sort level, after the while loop, __fill becomes log2(list.size())
list *__counter;
do {
__carry.splice(__carry.begin(), *this, begin()); // Place the first node of the current list at the beginning of the carry list
for (__counter = &__tmp[0];
__counter != __fill && !__counter->empty();
++__counter) {
__counter->merge(__carry); // Merge two sorted lists
__carry.swap(*__counter); // Swap the contents of the carry list and counter[i] list
}
__carry.swap(*__counter); // Swap the contents of the carry list and counter[i] list
if (__counter == __fill)
++__fill;
} while (!empty());
// Merge every two lists iteratively, ascending to the top, until *(__fill-1) stores the final sorted result. Then swap it into the current list.
for (__counter = &__tmp[1]; __counter != __fill; ++__counter)
__counter->merge(*(__counter - 1));
swap(*(__fill - 1));
}
}
The above code seems a bit difficult to understand. After searching online, I found the following code from G2.9:
template <class T, class Alloc>
void list<T, Alloc> :: sort(){
// Check if the list is empty or has only one element.
if(node->next == node || link_type(node->next)->next == node){
return;
}
list<T, Alloc> carry;
list<T, alloc> counter[64];
int fill = 0;
while(!empty()){
carry.splice(carry.begin(), *this, begin());
int i = 0;
while(i < fill && !counter[i].empty()){
counter[i].merge(carry);
carry.swap(counter[i++]);
}
carry.swap(counter[i]);
if(i == fill){
++fill;
}
}
for(int i = 1; i < fill; ++i){
counter[i].merge(counter[i-1]);
}
swap(counter[fill-1]);
}
The corresponding external implementation is:
void sortList(list<int> &l) {
if (l.size() <= 1) {
return;
}
list<int> carry; // Auxiliary list used to extract elements from 'a' and temporarily store the merge result of two lists
list<int> counter[64]; // Stores the result of each merge level, where the i-th list stores 2^i elements or 0
int fill = 0; // Represents the current maximum merge sort level, after the while loop, fill becomes log2(a.size())
while (!l.empty()) {
carry.splice(carry.begin(), l, l.begin()); // Move the first element of list 'a' to the beginning of carry list
int i = 0;
// Merge non-empty merge levels from small to large until an empty level is encountered or the current maximum merge level is reached
while (i < fill && !counter[i].empty()) {
counter[i].merge(carry); // Merge lists, the result list is sorted, and it must be ensured that the two lists to be merged are sorted before merging
carry.swap(counter[i++]); // Swap list elements
}
carry.swap(counter[i]);
if (i == fill) { // If i reaches the current maximum merge level, it means that a new level needs to be added
++fill;
}
}
for (int i = 1; i < fill; ++i) { // Merge the results of all merge levels to get the final result counter[fill - 1]
counter[i].merge(counter[i - 1]);
}
l.swap(counter[fill - 1]);
}
This part can refer to:
The blog provides a detailed process diagram.
Let's convert the G4.9 implementation to the corresponding external implementation again:
void sortList1(list<int> &l) {
typedef list<int> list;
if (l.size() <= 1) {
return;
}
list __carry;
list __tmp[64];
list *__fill = &__tmp[0];
list *__counter;
do {
__carry.splice(__carry.begin(), l, l.begin());
for (__counter = &__tmp[0];
__counter != __fill && !__counter->empty();
++__counter) {
__counter->merge(__carry);
__carry.swap(*__counter);
}
__carry.swap(*__counter);
if (__counter == __fill) ++__fill;
} while (!l.empty());
for (__counter = &__tmp[1]; __counter != __fill; ++__counter)
__counter->merge(*(__counter - 1));
l.swap(*(__fill - 1));
}
Usage:
int main() {
list<int> l = {7, 5, 8, 1};
cout << "===============Before Sorting==============" << endl;
for (auto i:l) cout << i << " ";
cout << endl;
sortList1(l);
cout << "===============After Sorting==============" << endl;
for (auto i:l) cout << i << " ";
cout << endl;
return 0;
}
Operator Overloading
template<typename _Tp, typename _Alloc>
inline bool
operator==(const list<_Tp, _Alloc> &__x, const list<_Tp, _Alloc> &__y) {
typedef typename list<_Tp, _Alloc>::const_iterator const_iterator;
const_iterator __end1 = __x.end();
const_iterator __end2 = __y.end();
const_iterator __i1 = __x.begin();
const_iterator __i2 = __y.begin();
while (__i1 != __end1 && __i2 != __end2 && *__i1 == *__i2) {
++__i1;
++__i2;
}
return __i1 == __end1 && __i2 == __end2;
}
``
`
The implementation idea is to iteratively check whether two iterators both reach the end.
The remaining part is the overloading of other operators, which are relatively simple and not elaborated here. Among them, `lexicographical_compare` is implemented in `c++-v3/src/c++98/stl_algobase.h`. This function tests whether [first1, last1) is less than [first2, last2) lexicographically. The function uses operator< or comp for comparison. Its behavior is similar to: if the two sequences have different lengths and the shorter sequence is identical to the beginning of the longer sequence (e.g., "example" and "examplee"), then the longer sequence is lexicographically larger than the shorter one.
```cpp
template <class InputIterator1, class InputIterator2>
bool lexicographical_compare (InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2)
{
while (first1!=last1)
{
if (first2==last2 || *first2<*first1) return false;
else if (*first1<*first2) return true;
++first1; ++first2;
}
return (first2!=last2);
}
Usage:
int main() {
vector<char> v1{'h','e','l','l','o'};
vector<char> v2{'h','e','l','l','o','o'};
vector<char> v3{'h','e','l','m','o'};
cout<<"v1=";
for(char i:v1)
cout<<i<<" ";
cout<<endl;
cout<<"v2=";
for(char i:v2)
cout<<i<<" ";
cout<<endl;
cout<<"v3=";
for(char i:v3)
cout<<i<<" ";
cout<<endl;
if(lexicographical_compare(v1.begin(),v1.end(),v2.begin(),v2.end()))
cout<<"v1 is less than v2 "<<endl;
else
cout<<"v2 is less than v1 "<<endl;
if(lexicographical_compare(v1.begin(),v1.end(),v3.begin(),v3.end()))
cout<<"v1 is less than v3 "<<endl;
else
cout<<"v3 is less than v1 "<<endl;
}
Other overloaded operators are as follows:
template<typename _Tp, typename _Alloc>
inline bool
operator<(const list<_Tp, _Alloc> &__x, const list<_Tp, _Alloc> &__y) {
return std::lexicographical_compare(__x.begin(), __x.end(),
__y.begin(), __y.end());
}
/// Based on operator==
template<typename _Tp, typename _Alloc>
inline bool
operator!=(const list<_Tp, _Alloc> &__x, const list<_Tp, _Alloc> &__y) { return !(__x == __y); }
/// Based on operator<
template<typename _Tp, typename _Alloc>
inline bool
operator>(const list<_Tp, _Alloc> &__x, const list<_Tp, _Alloc> &__y) { return __y < __x; }
/// Based on operator<
template<typename _Tp, typename _Alloc>
inline bool
operator<=(const list<_Tp, _Alloc> &__x, const list<_Tp, _Alloc> &__y) { return !(__y < __x); }
/// Based on operator<
template<typename _Tp, typename _Alloc>
inline bool
operator>=(const list<_Tp, _Alloc> &__x, const list<_Tp, _Alloc> &__y) { return !(__x < __y); }
1.2 List Base Source Code
In _list_base, there is a structure: _List_impl, and _List_impl has a _List_node_base.
class _List_base
{
protected:
typedef typename _Alloc::template rebind<_List_node<_Tp> >::other
_Node_alloc_type;
typedef typename _Alloc::template rebind<_Tp>::other _Tp_alloc_type;
struct _List_impl
: public _Node_alloc_type
{
__detail::_List_node_base _M_node;
_List_impl()
: _Node_alloc_type(), _M_node()
{ }
_List_impl(const _Node_alloc_type& __a) _GLIBCXX_NOEXCEPT
: _Node_alloc_type(__a), _M_node()
{ }
#if __cplusplus >= 201103L
_List_impl(_Node_alloc_type&& __a) _GLIBCXX_NOEXCEPT
: _Node_alloc_type(std::move(__a)), _M_node()
{ }
#endif
};
_List_impl _M_impl;
};
The final diagram is:
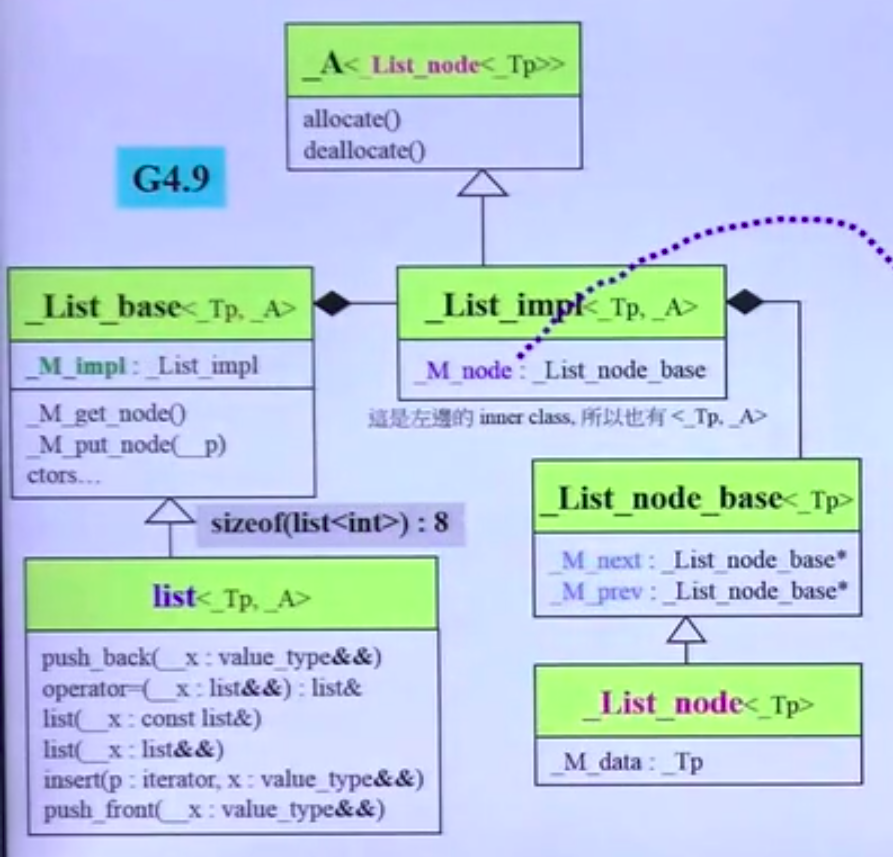
So, if we want to calculate:
sizeof(list<int>)=16
The reason is:
The sizeof list is 1, so the sizeof comes from the base class _list_base, and in _list_base, there is a structure: _List_impl, and in _List_impl, there is a _List_node_base.
We know that _List_node_base has two pointers. On a 64-bit system, each pointer is 8 bytes, totaling 16 bytes.
2. Analysis of List's Iterator
2.1 iterator
Definition of the iterator for a list:
template<typename _Tp>
struct _List_iterator
{
typedef _List_iterator<_Tp> _Self;
typedef _List_node<_Tp> _Node;
typedef ptrdiff_t difference_type;
typedef std::bidirectional_iterator_tag iterator_category;
typedef _Tp value_type;
typedef _Tp* pointer;
typedef _Tp& reference;
// The only member points to the %list element.
__detail::_List_node_base* _M_node;
// _List_node (data part of the node) -> _List_node_base (previous and next pointers)
_List_iterator() _GLIBCXX_NOEXCEPT
: _M_node() { }
explicit
_List_iterator(__detail::_List_node_base* __x) _GLIBCXX_NOEXCEPT
: _M_node(__x) { }
_Self
_M_const_cast() const _GLIBCXX_NOEXCEPT
{ return *this; }
// The only member points to the %list element.
__detail::_List_node_base* _M_node;
};
Internal Overloaded Functions:
// Must downcast from _List_node_base to _List_node to get to _M_data.
// Overload * operator
reference operator*() const _GLIBCXX_NOEXCEPT
{
return static_cast<_Node*>(_M_node)->_M_data;
}
// Overload -> operator
pointer operator->() const _GLIBCXX_NOEXCEPT
{
return std::__addressof(static_cast<_Node*>(_M_node)->_M_data);
}
// Overload prefix ++ operator ++i
_Self& operator++() _GLIBCXX_NOEXCEPT
{
_M_node = _M_node->_M_next;
return *this;
}
// Overload postfix ++ operator i++
_Self operator++(int) _GLIBCXX_NOEXCEPT
{
_Self __tmp = *this; // Record the original value * calls the copy constructor
_M_node = _M_node->_M_next; // Perform operation
return __tmp; // Return the original value
}
// Overload prefix -- operator --i
_Self& operator--() _GLIBCXX_NOEXCEPT
{
_M_node = _M_node->_M_prev;
return *this;
}
// Overload postfix -- operator --i
_Self operator--(int) _GLIBCXX_NOEXCEPT
{
_Self __tmp = *this;
_M_node = _M_node->_M_prev;
return __tmp;
}
// Overload ++ operator
bool operator==(const _Self& __x) const _GLIBCXX_NOEXCEPT
{
return _M_node == __x._M_node;
}
// Overload != operator
bool operator!=(const _Self& __x) const _GLIBCXX_NOEXCEPT
{
return _M_node != __x._M_node;
}
2.2 Node Design
The _List_node within the iterator inherits from _List_node_base.
_List_node holds the data part.
_List_node_base holds the pointers to the previous and next nodes.
/// An actual node in the %list.
template<typename _Tp>
struct _List_node : public __detail::_List_node_base
{
///< User's data.
_Tp _M_data;
#if __cplusplus >= 201103L
template<typename... _Args>
_List_node(_Args&&... __args)
: __detail::_List_node_base(), _M_data(std::forward<_Args>(__args)...)
{ }
#endif
};
_List_node_base code:
namespace __detail
{
_GLIBCXX_BEGIN_NAMESPACE_VERSION
/// Common part of a node in the %list.
struct _List_node_base
{
_List_node_base* _M_next;
_List_node_base* _M_prev;
static void
swap(_List_node_base& __x, _List_node_base& __y) _GLIBCXX_USE_NOEXCEPT;
void
_M_transfer(_List_node_base* const __first,
_List_node_base* const __last) _GLIBCXX_USE_NOEXCEPT;
void
_M_reverse() _GLIBCXX_USE_NOEXCEPT;
void
_M_hook(_List_node_base* const __position) _GLIBCXX_USE_NOEXCEPT;
void
_M_unhook() _GLIBCXX_USE_NOEXCEPT;
};
_GLIBCXX_END_NAMESPACE_VERSION
} // namespace detail
When designing the iterator, it always follows the principle of front-closed and back-open. For example, iter->begin() points to the first element, iter->end() points to the next element after the actual last element, hence the deliberate addition of a blank node at the end of the circular list to adhere to the STL front-closed and back-open principle.