- Published on
Exploring the C++ STL Source Code: The Story of set and multiset
- Authors

- Name
- light-city
Exploring the C++ STL Source Code: The Story of set and multiset
set/multiset uses rb_tree as the underlying data structure, which gives them automatic sorting capabilities. The sorting is based on the key, and the value of set/multiset elements is the same as the key.
We cannot use iterators of set/multiset to change the value of elements (because the key has its strict ordering rules). The iterators of set/multiset are const_iterators of the underlying RB tree, explicitly designed to prevent users from modifying elements.
The key of set elements must be unique, so the insert function of set uses insert_unique() of rb_tree. On the other hand, the key of multiset elements can be duplicated, so the insert function of multiset uses insert_equal() of rb_tree.
1. set
Let's start with a few questions regarding the set source code.
First question: The key is the value, and the value is the key.
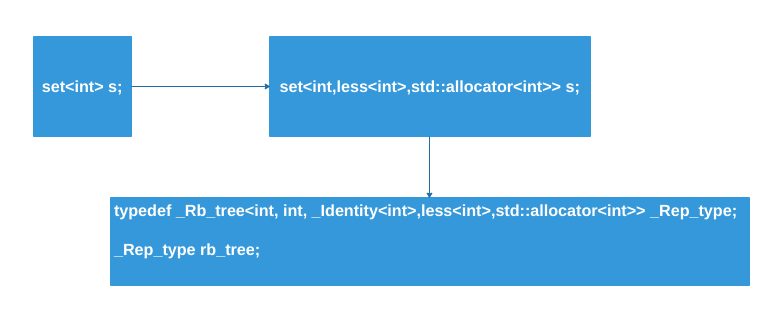
The specific code will be shown in the second question, but here is the internal logic we usually write in code. We can see that there is a red-black tree inside, and the definition of the red-black tree has the key and value as the same type, answering this question. (The typedefs in the source code are all derived from the key).
template<typename _Key, typename _Compare = std::less<_Key>,
typename _Alloc = std::allocator<_Key> >
class set
{
// concept requirements
typedef typename _Alloc::value_type _Alloc_value_type;
public:
// typedefs:
//@{
/// Public typedefs.
typedef _Key key_type;
typedef _Key value_type; // value is also the key
typedef _Compare key_compare;
typedef _Compare value_compare;
typedef _Alloc allocator_type;
//@}
private:
typedef _Rb_tree<key_type, value_type, _Identity<value_type>,
key_compare, _Key_alloc_type> _Rep_type;
_Rep_type _M_t; // Red-black tree representing set.
};
Second question: We cannot change the value of elements using iterators.
By examining the iterators used in the code, we find that they are all const_iterator, which answers the second question.
template<typename _Key, typename _Compare = std::less<_Key>,
typename _Alloc = std::allocator<_Key> >
class set
{
private:
typedef _Rb_tree<key_type, value_type, _Identity<value_type>,
key_compare, _Key_alloc_type> _Rep_type;
_Rep_type _M_t; // Red-black tree representing set.
public:
typedef typename _Rep_type::const_iterator iterator;
typedef typename _Rep_type::const_iterator const_iterator;
typedef typename _Rep_type::const_reverse_iterator reverse_iterator;
typedef typename _Rep_type::const_reverse_iterator const_reverse_iterator;
};
Based on the analysis above, we are reminded of queue, priority_queue, and stack. They all use the underlying container, making them container adapters. Similarly, set also uses the underlying container, so it can be called a container adapter.
Third question: The insert operation is unique for each key.
The underlying code calls _M_insert_unique() for insertion.
template<typename _InputIterator>
set(_InputIterator __first, _InputIterator __last)
: _M_t()
{ _M_t._M_insert_unique(__first, __last); }
Let's take a brief look at the implementation of this function: The _M_get_insert_unique_pos function returns a pair. If the inserted key is the same, the second element of the pair is 0. By checking whether it is 0, we can determine if the key is duplicated. In the code below, when the second element is not 0, indicating no duplication, we can directly insert the element by constructing a pair with second set to true. Otherwise, construct a pair with second set to false.
template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc>
#if __cplusplus >= 201103L
template<typename _Arg>
#endif
pair<typename _Rb_tree<_Key, _Val, _KeyOfValue,
_Compare, _Alloc>::iterator, bool>
_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::
_M_insert_unique( _Arg && __v )
{
typedef pair<iterator, bool> _Res;
pair<_Base_ptr, _Base_ptr> __res
= _M_get_insert_unique_pos( _KeyOfValue() ( __v ) );
if ( __res.second )
return(_Res( _M_insert_( __res.first, __res.second,
_GLIBCXX_FORWARD( _Arg, __v ) ),
true ) );
return(_Res( iterator( static_cast<_Link_type>(__res.first) ), false ) );
}
The usage of the above pair gives me an inspiration. It turns out that it can be used like this. Let's learn from it:
cout<<"flag: "<<itree._M_insert_unique(5).second<<endl; // Learn about the return value
typedef pair<int ,bool> _Res; // Also use typedef for pair
cout<<_Res(1,true).first<<endl; // Directly wrap it
_Res r=make_pair(2,false); // Define a new object
cout<<r.first<<endl; // Output the result
2. Multiset
Similarly, the definition of multiset is basically similar to set. The difference lies in the use of another function for insertion, which enables it to handle the insertion of duplicate keys!
template<typename _InputIterator>
multiset(_InputIterator __first, _InputIterator __last)
: _M_t()
{ _M_t._M_insert_equal(__first, __last); }
Now let's analyze _M_insert_equal:
typename _Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::iterator
_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::
_M_insert_equal(_Arg&& __v)
{
pair<_Base_ptr, _Base_ptr> __res = _M_get_insert_equal_pos(_KeyOfValue()(__v));
return _M_insert_(__res.first, __res.second, _GLIBCXX_FORWARD(_Arg, __v));
}
Next, we continue to trace the function _M_get_insert_equal_pos mentioned above:
template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc>
pair<typename _Rb_tree<_Key, _Val, _KeyOfValue,
_Compare, _Alloc>::_Base_ptr,
typename _Rb_tree<_Key, _Val, _KeyOfValue,
_Compare, _Alloc>::_Base_ptr>
_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::
_M_get_insert_equal_pos(const key_type& __k)
{
typedef pair<_Base_ptr, _Base_ptr> _Res;
_Link_type __x = _M_begin();
_Link_type __y = _M_end();
while (__x != 0)
{
__y = __x;
__x = _M_impl._M_key_compare(__k, _S_key(__x)) ?
_S_left(__x) : _S_right(__x);
}
return _Res(__x, __y);
}
Upon comparing these functions between multiset and set, it is apparent that the returned pair has significant differences. For the previous set, it needs to return whether the insertion was successful, because the key must be unique. In contrast, multiset does not need to indicate whether the insertion was successful. Therefore, the pair does not contain a bool type, making it directly return a pair consisting of the insertion point. Thus, compared to before, no matter how many keys there are and regardless of duplication, they can all be inserted.