- Published on
算法从0到1之trie(字典树)的增删改查(递归与非递归实现)
- Authors

- Name
- light-city
算法从0到1之trie(字典树)的增删改查(递归与非递归实现)
Table of Contents
0.导语
Trie树,又称单词查找树或键树,是一种树形结构。典型应用是用于统计和排序大量的字符串(但不仅限于字符串)。Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。 Trie树的基本性质可以归纳为:
- 根节点不包含字符,除根节点意外每个节点只包含一个字符。
- 从根节点到某一个节点,路径上经过的字符连接起来,为一个字符串。
- 假设所有字符串长度之和为n,构建字典树的时间复杂度为O(n)。 假设要查找的字符串长度为k,查找的时间复杂度为O(k)。
本节目标:从0到1构建下面trie树。完成trie的增删改查,统计单词词频与是否包含前缀等功能!
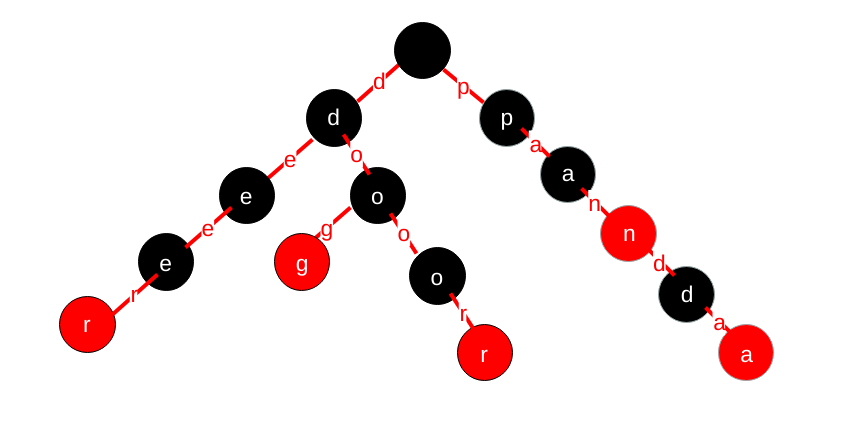
1.数据结构与类封装
1.1 数据结构定义
看上图可以发现,对于每个节点来说我们可以不用保存值,我们也需要知道词频,以及判断此时是否是单词。 因此数据结构定义如下:
class Trie {
private:
struct Node { // Node节点并不需要存储当前字符是谁
int value = 0; // 当前节点的词频
bool isWord = false;
map<char, Node *> next;
};
};
上述map中key为当前节点,value为下一个节点。
1.2 类的封装
构造函数定义:
class Trie {
private:
Node *root;
int size;
public:
Trie() {
root = new Node();
size = 0;
}
// 获取 Trie中存储的单词数量
int getSize() {
return size;
}
};
2.具体功能实现
2.1 插入节点
非递归
思路:遍历word的每个字符,如果在Trie树中存在,就往下查找,否则插入节点:
其中value表示当前单词的词频统计,如果之前单词存在,直接++,否则为1,isWord为表示是否是单词。
public:
// 非递归
// 添加新的单词word
void add(string word) {
Node *cur = root;
for (int i = 0; i < word.size(); i++) {
char c = word[i];
if (cur->next.count(c) == 0)
cur->next.insert(make_pair(c, new Node()));
cur = cur->next.at(c);
}
if (cur->isWord == false) { // 添加的是个新单词
cur->isWord = true;
cur->value = 1;
size++;
} else { // 之前单词存在
cur->value++;
}
}
递归实现
首先定义一个开放接口:
public:
// 递归添加
void _add(string word) {
add(word, 0, root);
}
屏蔽内部实现:具体思路同上树非递归,就是将循环改为递归即可。
private:
// 添加word
void add(string word, int index, Node *node) {
Node *cur = node;
if (index == word.size()) {
if (cur->isWord == false) { // 添加的是个新单词
cur->value = 1;
cur->isWord = true;
size++;
} else {
cur->value++;
}
return;
}
char c = word[index];
if (cur->next.count(c) == 0)
cur->next.insert(make_pair(c, new Node()));
add(word, index + 1, node->next.at(c));
return;
}
2.2 是否包含单词
非递归
其中要注意的是,当for循环结束后,应该返回的是isWord,而不能直接返回true,原因是比如trie树中有pandas 这个单词,但要查pan这个单词,此时应该返回false,而不是true。
public:
// 非递归 是否包含word
bool contain(string word) {
Node *cur = root;
for (int i = 0; i < word.size(); i++) {
char c = word[i];
// not found
if (cur->next.count(c) == 0) return false;
cur = cur->next.at(c);
}
return cur->isWord; // 比如trie树中有pandas 这个单词,但要查pan这个单词,此时应该返回cur->isWord,而不是true。
}
递归
public:
// 递归 是否包含word
bool _contain(string word) {
return contain(word, 0, root);
}
private:
// 是否包含word
bool contain(string word, int index, Node *node) {
Node *cur = node;
if (index == word.size())
return cur->isWord; // 注意!!!
char c = word[index];
if (cur->next.count(c) == 0)
return false;
return contain(word, index + 1, node->next.at(c));
}
2.3 查询在Trie树中是否有以prefix为前缀的单词
这个就刚好是把上述的那个注意地方改为true即可。
非递归实现
public:
// 查询是否在Trie中有单词以prefix为前缀
bool isPrefix(string prefix) {
Node *cur = root;
for (int i = 0; i < prefix.size(); i++) {
char c = prefix[i];
// not found
if (cur->next.count(c) == 0) return false;
cur = cur->next.at(c);
}
return true;
}
递归实现
public:
// 非递归查询是否在Trie中有单词以prefix为前缀
bool _isPrefix(string prefix) {
return isPrefix(prefix, 0, root);
}
private:
// 是否包含前缀
bool isPrefix(string word, int index, Node *node) {
Node *cur = node;
if (index == word.size())
return true;
char c = word[index];
if (cur->next.count(c) == 0)
return false;
return isPrefix(word, index + 1, node->next.at(c));
}
2.4 删除单词
删除单词分为两种情况。
第一种情况:当当前单词最后字符无孩子,那么自底向上删除,自底向上删除要注意有没有分叉,如果有分叉,则从分叉处往上不做修改,否则就要释放内存,删除节点。例如上图

我们要删除door单词,自r往上递归删除的时候当删除到第二个o的时候,有两个分支,此时我们不应该把o的内存删掉,而应该从这个节点开始不操作,因为操作了的化,dog单词也就不存在了。
第二种情况:当前单词最后字符有孩子,那么直接将当前单子最后字符的isWord设为false即可,如上图删除pan,只需要将n变黑即可,而不应该释放pan的内存,一旦释放,后面便没法访问到panda。
下面来实现:
首先定义两个遍历,分别存储是否自底向上删除,也就是上述door删除操作为r->o->o->d,另一个为是否停止向上删除,这个表示当自底向上删除door,到了第二个o的时候有其他分叉,那么在往回递归就不操作了。
public:
bool islast = false; // 是否自底向上
bool isstop = false; // 是否停止向上删除
删除单词实现:
public:
void remove(string word) {
Node *cur = root;
for (int i = 0; i < word.size(); i++) {
char c = word[i];
if (cur->next.count(c) == 0) return;
cur = cur->next.at(c);
}
// 到达删除被删除单词的最后一个字符
if (cur->next.size() == 0) { // 后面无节点,则自底向上删除
__del(word, 0, root);
} else { // 后面有节点,直接标记当前节点不是单词即可
cur->isWord = false;
}
size--;
//恢复flag,否则只能删除1次,不能够连续删除!
islast= false;
isstop=false;
}
其中有个函数__del来处理自底向上删除节点操作:
private:
void __del(string word, int index, Node *node) {
char c = word[index];
if (word.size() - 1 == index) {
islast = true;
free(node->next.at(c));
node->next.erase(c);
return;
}
if (!isstop && islast) {
// 后面有分叉或者当前节点是单词
if (node->next.size() >= 2 || node->isWord == true)
isstop = true;
free(node->next.at(c));
node->next.erase(c);
}
__del(word, index + 1, node->next.at(c));
}
2.5 统计词频
直接往下查找,直到最后的节点,返回value即可。
public:
// 获取单词的词频
int getVal(string word) {
Node *cur = root;
for (int i = 0; i < word.size(); i++) {
char c = word[i];
if (cur->next.count(c) == 0) return 0;
cur = cur->next.at(c);
}
return cur->value;
}
递归操作就不阐述了,代码与上述的包含,添加逻辑类似。
3.测试
编写main函数:
#include "trie.h"
int main() {
Trie *trie=new Trie();
trie->_add("deer");
trie->_add("door");
trie->_add("dog");
trie->_add("panda");
trie->_add("pan");
trie->_add("pan");
cout<<trie->getSize()<<endl; // 5
cout<<trie->getVal("pan")<<endl; // 2
cout<<trie->contain("pan")<<endl; // 1
cout<<trie->_contain("door")<<endl; // 1
cout<<trie->isPrefix("pan")<<endl; // 1
cout<<trie->_isPrefix("pan")<<endl; // 1
cout<<trie->isPrefix("pag")<<endl; // 0
cout<<trie->_isPrefix("pag")<<endl; // 0
trie->remove("deer");
cout<<trie->_contain("deer")<<endl; // 0
cout<<trie->_contain("dog")<<endl; // 1
cout<<trie->_contain("door")<<endl; // 1
cout<<trie->getSize()<<endl; // 4
trie->remove("door");
cout<<trie->_contain("door")<<endl; // 0
cout<<trie->_contain("dog")<<endl; // 1
cout<<trie->getSize()<<endl; // 3
trie->remove("pan");
cout<<trie->_contain("pan")<<endl; // 0
cout<<trie->_contain("panda")<<endl;// 1
cout<<trie->getSize()<<endl; // 2
trie->remove("panda");
cout<<trie->_contain("panda")<<endl;// 0
cout<<trie->_contain("pan")<<endl; // 0
cout<<trie->getSize()<<endl; // 1
delete trie;
return 0;
}
对比测试结果,函数测试完毕,正确!